- Xe Has How Many Valence Electrons
- List Of Valence Electrons For Each Element
- Xe Valence Electrons And Core Electrons
Identify the number of core and valence electrons for each atom. Xe: core electrons Xe: valence electrons Be: core electrons Be: valence electrons Br: core electrons Br: valence elect. Xe6s24f145d106p2 Xe6s25d106p2 Xe6s24f145d106p2. Hydrogen reacts with an element to form a compound. Which element would have the most electrons available to react with hydrogen? They have more valence electrons available for bonding. Their electrons are assigned to s and p orbitals only. How many valence electrons does lithium (Li. Xe does not follow the octet rule. It actually bonds. It will hold more than 8 electrons. Xenon having valence electrons in the 4th energy level, will also have access to the 4d sublevel, thus allowing for more than 8 electrons. XeF 2 is dsp 3 hybridized and contains 3 lone pair and 2 bonding pairs of valence electrons around the Xenon.
Xe Has How Many Valence Electrons
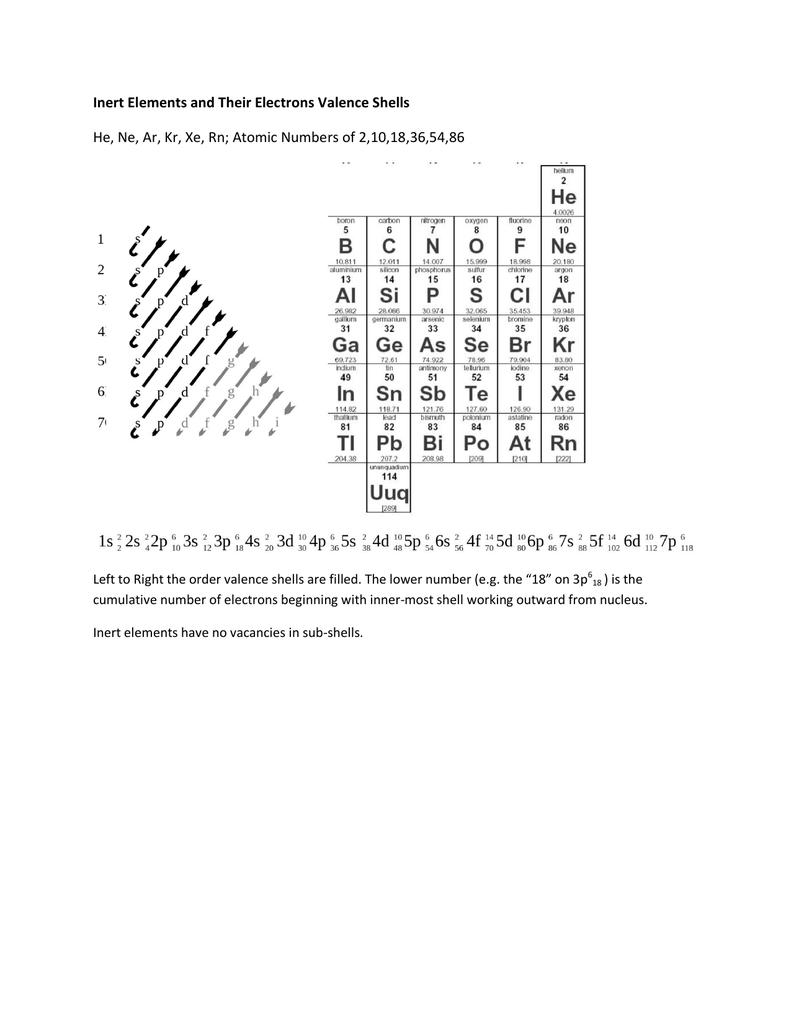
Helium is an exception: despite having a 1s 2 configuration with two valence electrons, and thus having some similarities with the alkaline earth metals with their ns 2 valence configurations, its shell is completely full and hence it is chemically very inert and is usually placed in group 18 with the other noble gases. Xenon's valence shell, or outermost energy level of electrons, contains 8 electrons, and it is the 5th energy level of that atom. Xenon is a noble gas, so it is naturally inert.
Learning Objectives Ewoks complete series.
- To understand the basics of adding electrons to atomic orbitals
- To understand the basics of the Aufbau principle
The electron configuration of an element is the arrangement of its electrons in its atomic orbitals. By knowing the electron configuration of an element, we can predict and explain a great deal of its chemistry.
The Aufbau Principle
List Of Valence Electrons For Each Element
We construct the periodic table by following the aufbau principle (from German, meaning “building up”). First we determine the number of electrons in the atom; then we add electrons one at a time to the lowest-energy orbital available without violating the Pauli principle. We use the orbital energy diagram of Figure (PageIndex{1}), recognizing that each orbital can hold two electrons, one with spin up ↑, corresponding to ms = +½, which is arbitrarily written first, and one with spin down ↓, corresponding to ms = −½. A filled orbital is indicated by ↑↓, in which the electron spins are said to be paired. Here is a schematic orbital diagram for a hydrogen atom in its ground state:


From the orbital diagram, we can write the electron configuration in an abbreviated form in which the occupied orbitals are identified by their principal quantum number n and their value of l (s, p, d, or f), with the number of electrons in the subshell indicated by a superscript. For hydrogen, therefore, the single electron is placed in the 1s orbital, which is the orbital lowest in energy (Figure (PageIndex{1})), and the electron configuration is written as 1s1 and read as “one-s-one.”
A neutral helium atom, with an atomic number of 2 (Z = 2), has two electrons. We place one electron in the orbital that is lowest in energy, the 1s orbital. From the Pauli exclusion principle, we know that an orbital can contain two electrons with opposite spin, so we place the second electron in the same orbital as the first but pointing down, so that the electrons are paired. The orbital diagram for the helium atom is therefore
Xe Valence Electrons And Core Electrons

written as 1s2, where the superscript 2 implies the pairing of spins. Otherwise, our configuration would violate the Pauli principle.
The next element is lithium, with Z = 3 and three electrons in the neutral atom. We know that the 1s orbital can hold two of the electrons with their spins paired; the third electron must enter a higher energy orbital. Figure 6.29 tells us that the next lowest energy orbital is 2s, so the orbital diagram for lithium is
This electron configuration is written as 1s22s1.
The next element is beryllium, with Z = 4 and four electrons. We fill both the 1s and 2s orbitals to achieve a 1s22s2 electron configuration:
When we reach boron, with Z = 5 and five electrons, we must place the fifth electron in one of the 2p orbitals. Because all three 2p orbitals are degenerate, it doesn’t matter which one we select. The electron configuration of boron is 1s22s22p1:
At carbon, with Z = 6 and six electrons, we are faced with a choice. Should the sixth electron be placed in the same 2p orbital that already has an electron, or should it go in one of the empty 2p orbitals? If it goes in an empty 2p orbital, will the sixth electron have its spin aligned with or be opposite to the spin of the fifth? In short, which of the following three orbital diagrams is correct for carbon, remembering that the 2p orbitals are degenerate?
Because of electron-electron interactions, it is more favorable energetically for an electron to be in an unoccupied orbital than in one that is already occupied; hence we can eliminate choice a. Similarly, experiments have shown that choice b is slightly higher in energy (less stable) than choice c because electrons in degenerate orbitals prefer to line up with their spins parallel; thus, we can eliminate choice b. Choice c illustrates Hund’s rule (named after the German physicist Friedrich H. Hund, 1896–1997), which today says that the lowest-energy electron configuration for an atom is the one that has the maximum number of electrons with parallel spins in degenerate orbitals. By Hund’s rule, the electron configuration of carbon, which is 1s22s22p2, is understood to correspond to the orbital diagram shown in c. Experimentally, it is found that the ground state of a neutral carbon atom does indeed contain two unpaired electrons.
When we get to nitrogen (Z = 7, with seven electrons), Hund’s rule tells us that the lowest-energy arrangement is

with three unpaired electrons. The electron configuration of nitrogen is thus 1s22s22p3.
At oxygen, with Z = 8 and eight electrons, we have no choice. One electron must be paired with another in one of the 2p orbitals, which gives us two unpaired electrons and a 1s22s22p4 electron configuration. Because all the 2p orbitals are degenerate, it doesn’t matter which one has the pair of electrons.
Similarly, fluorine has the electron configuration 1s22s22p5:
When we reach neon, with Z = 10, we have filled the 2p subshell, giving a 1s22s22p6 electron configuration:
Notice that for neon, as for helium, all the orbitals through the 2p level are completely filled. This fact is very important in dictating both the chemical reactivity and the bonding of helium and neon, as you will see.
